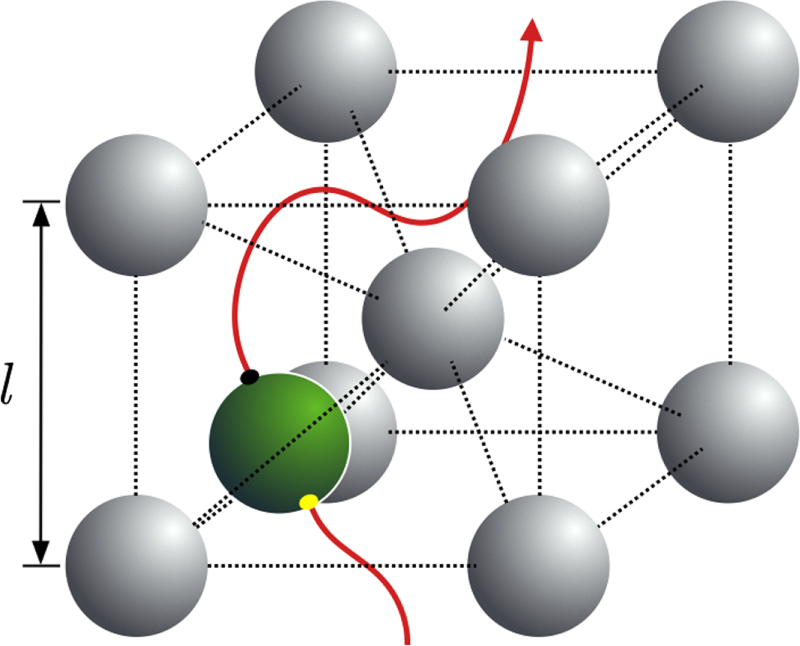
Active particles in periodic lattices
Both natural and artificial small-scale swimmers may often self-propel in environments subject to complex geometrical constraints. While most past theoretical work on low-Reynolds number locomotion addressed idealised geometrical situations, not much is known on the motion of swimmers in heterogeneous environments. As a first theoretical model, we investigate numerically the behaviour of a single spherical micro-swimmer located in an infinite, periodic body-centred cubic lattice consisting of rigid inert spheres of the same size as the swimmer. Running a large number of simulations we uncover the phase diagram of possible trajectories as a function of the strength of the swimming actuation and the packing density of the lattice. We then use hydrodynamic theory to rationalise our computational results and show in particular how the far-field nature of the swimmer (pusher versus puller) governs even the behaviour at high volume fractions.