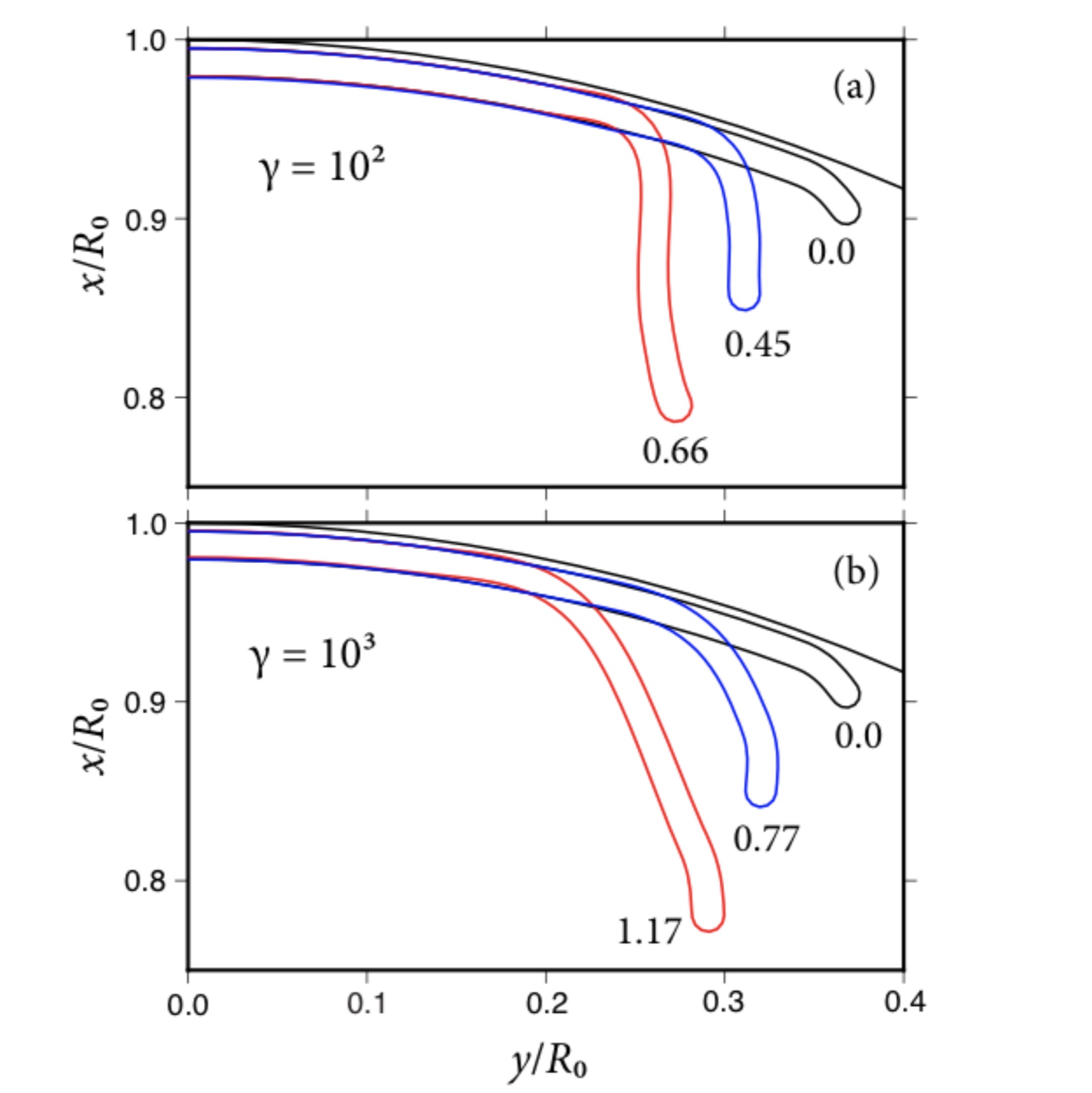
To understand how a spherical geometry influences the dynamics of gravity-driven subduction of the oceanic lithosphere on Earth, we study a simple model of a thin and dense axisymmetric shell of thickness h and viscosity η_1 sinking in a spherical body of fluid with radius R_0 and a lower viscosity η_0. Using scaling analysis based on thin viscous shell theory, we identify a fundamental length scale, the ‘bending length’ l_b, and two key dimensionless parameters that control the dynamics: the ‘flexural stiffness’ St=(η_1/η_0)(h/l_b)^3 and the ‘sphericity number’ Σ=(l_b/R_0)cot(θ_t), where θ_t is the angular radius of the subduction trench. To validate the scaling analysis, we obtain a suite of instantaneous numerical solutions using a boundary-element method based on new analytical point-force Green functions that satisfy free-slip boundary conditions on the sphere’s surface. To isolate the effect of sphericity, we calculate the radial sinking speed V and the hoop stress resultant T_2 at the leading end of the subducted part of the shell, both normalised by their ‘flat-Earth’ values (i.e. for Σ=0). For reasonable terrestrial values of η_1/η_0 (≈ several hundred), sphericity has a modest effect on V, which is reduced by <7% for large plates such as the Pacific plate and by up to 34 % for smaller plates such as the Cocos and Philippine Sea plates. However, sphericity has a much greater effect on T_2 increasing it by up to 64 % for large plates and 240 % for small plates. This result has important implications for the growth of longitudinal buckling instabilities in subducting spherical shells.