Article
Publication Types:
Fluid mechanics of free subduction on a sphere, 1: The axisymmetric case
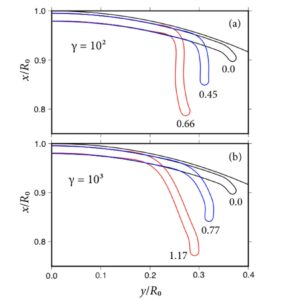
To understand how a spherical geometry influences the dynamics of gravity-driven subduction of the oceanic lithosphere on Earth, we study a simple model of a thin and dense axisymmetric shell of thickness h and viscosity η_1 sinking in a spherical body of fluid with radius R_0 and a lower viscosity η_0. Using scaling analysis based on thin viscous shell theory, we identify a fundamental length scale, the ‘bending length’ l_b, and two key dimensionless parameters that control the dynamics: the ‘flexural stiffness’ St=(η_1/η_0)(h/l_b)^3 and the ‘sphericity number’ Σ=(l_b/R_0)cot(θ_t), where θ_t is the angular radius of the subduction trench. To validate the scaling analysis, we obtain a suite of instantaneous numerical solutions using a boundary-element method based on new analytical point-force Green functions that satisfy free-slip boundary conditions on the sphere’s surface. To isolate the effect of sphericity, we calculate the radial sinking speed V and the hoop stress resultant T_2 at the leading end of the subducted part of the shell, both normalised by their ‘flat-Earth’ values (i.e. for Σ=0). For reasonable terrestrial values of η_1/η_0 (≈ several hundred), sphericity has a modest effect on V, which is reduced by <7% for large plates such as the Pacific plate and by up to 34 % for smaller plates such as the Cocos and Philippine Sea plates. However, sphericity has a much greater effect on T_2 increasing it by up to 64 % for large plates and 240 % for small plates. This result has important implications for the growth of longitudinal buckling instabilities in subducting spherical shells.

Stokes flow due to point torques and sources in a spherical geometry
Solutions to the Stokes equations written in terms of a small number of hydrodynamic image singularities have been a useful tool in theoretical and numerical computations for nearly 50 years. In this article, we extend the catalog of known solutions by deriving the flow expressions due to a general point torque and point source in the presence of a stationary sphere with either a no-slip or a stress-free (no-shear) boundary condition. For an axisymmetric point torque and a no-slip sphere the image system simplifies to a single image point torque, reminiscent of the solution for a point charge outside an equipotential sphere in electrostatics. By symmetry, this also gives a simple representation of the solution due to an axisymmetric point torque inside a rigid spherical shell. In all remaining cases, the solution can be described by a collection of physically intuitive point and line singularities. Our results will be useful for the theoretical modeling of the propulsion of microswimmers and efficient numerical implementation of far-field hydrodynamic interactions in this geometry.
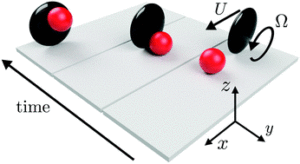
Irreversible hydrodynamic trapping by surface rollers
A colloidal particle driven by externally actuated rotation can self-propel parallel to a rigid boundary by exploiting the hydrodynamic coupling that surfaces induce between translation and rotation. As such a roller moves along the boundary it generates local vortical flows, which can be used to trap and transport passive cargo particles. However, the details and conditions for this trapping mechanism have not yet been fully understood. Here, we show that the trapping of cargo is accomplished through time-irreversible interactions between the cargo and the boundary, leading to its migration across streamlines into a steady flow vortex next to the roller. The trapping mechanism is explained analytically with a two dimensional model, investigated numerically in three dimensions for a wide range of parameters and is shown to be analogous to the deterministic lateral displacement (DLD) technique used in microfluidics for the separation of differently sized particles. The several geometrical parameters of the problem are analysed and we predict that thin, disc-like rollers offer the most favourable trapping conditions.
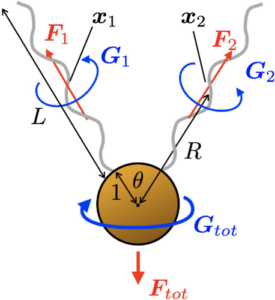
Direct versus indirect hydrodynamic interactions during bundle formation of bacterial flagella
Most motile bacteria swim in viscous fluids by rotating multiple helical flagellar filaments. These semirigid filaments repeatedly join (“bundle”) and separate (“unbundle”), resulting in a two-gait random-walk-like motion of the cell. In this process, hydrodynamic interactions between the filaments are known to play an important role and can be categorized into two distinct types: direct interactions mediated through flows that are generated through the actuation of the filaments themselves, and indirect interactions mediated through the motion of the cell body (i.e., flows induced in the swimming frame that result from propulsion). To understand the relative importance of these two types of interactions, we study a minimal singularity model of flagellar bundling. Using hydrodynamic images, we solve for the flow analytically and compute both direct and indirect interactions exactly as a function of the length of the flagellar filaments and their angular separation. We show (i) that the generation of thrust by flagella alone is sufficient to drive the system towards a bundled state through both types of interaction in the entire geometric parameter range; (ii) that for both thrust- and rotation-induced flows indirect advection dominates for long filaments and at wide separation, i.e., primarily during the early stages of the bundling process; and (iii) that, in contrast, direct interactions dominate when flagellar filaments are in each other’s wake, which we characterize mathematically. We further introduce a numerical elastohydrodynamic model that allows us to compute the dynamics of the helical axes of each flagellar filament while analyzing direct and indirect interactions separately. With this we show (iv) that the shift in balance between direct and indirect interactions is nonmonotonic during the bundling process, with a peak in direct dominance, and that different sections of the flagella are affected by these changes to different extents.
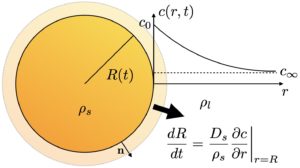
Stochastic dynamics of dissolving active particles
The design of artificial microswimmers has generated significant research interest in recent years, for promise in applications such as nanomotors and targeted drug-delivery. However, many current designs suffer from a common problem, namely the swimmers remain in the fluid indefinitely, posing risks of clogging and damage. Inspired by recently proposed experimental designs, we investigate mathematically the dynamics of degradable active particles. We develop and compare two distinct chemical models for the decay of a swimmer, taking into account the material composition and nature of the chemical or enzymatic reaction at its surface. These include a model for dissolution without a reaction, as well as models for a reacting swimmer studied in the limit of large and small Damköhler number. A new dimensionless parameter emerges that allows the classification of colloids into ballistic and diffusive type. Using this parameter, we perform an asymptotic analysis to derive expressions for colloid lifetimes and their total mean squared displacement from release and validate these by numerical Monte Carlo simulations of the associated Langevin dynamics. Supported by general scaling relationships, our theoretical results provide new insight into the experimental applicability of a wide range of designs for degradable active colloids.
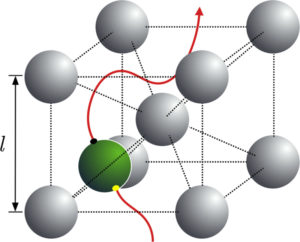
Active particles in periodic lattices
Both natural and artificial small-scale swimmers may often self-propel in environments subject to complex geometrical constraints. While most past theoretical work on low-Reynolds number locomotion addressed idealised geometrical situations, not much is known on the motion of swimmers in heterogeneous environments. As a first theoretical model, we investigate numerically the behaviour of a single spherical micro-swimmer located in an infinite, periodic body-centred cubic lattice consisting of rigid inert spheres of the same size as the swimmer. Running a large number of simulations we uncover the phase diagram of possible trajectories as a function of the strength of the swimming actuation and the packing density of the lattice. We then use hydrodynamic theory to rationalise our computational results and show in particular how the far-field nature of the swimmer (pusher versus puller) governs even the behaviour at high volume fractions.
